Manipulating Light (Chapter 4)
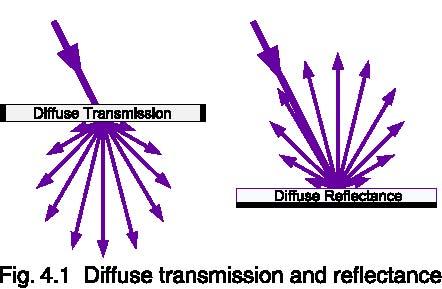
Diffusion
It is often necessary to diffuse light, either through transmission or reflection. Diffuse transmission can be accomplished by transmitting light through roughened quartz, flashed opal, or polytetrafluoroethylene (PTFE, Teflon). Diffusion can vary with wavelength. Teflon is a poor IR diffuser, but makes an excellent visible / UV diffuser. Quartz is required for IR diffusion.
Integrating spheres are coated with BaSO4 or PTFE, which offer >97% reflectance over a broad spectral range with near perfect diffusion. These coatings are, however, quite expensive and fragile.
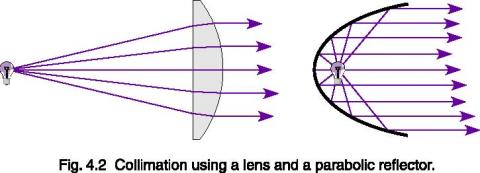
Collimation
Some lamps use collimating lenses or reflectors to redirect light into a beam of parallel rays. If the lamp filament is placed at the focal point of the lens, all rays entering the lens will become parallel. Similarly, a lamp placed in the focal point of a spherical or parabolic mirror will project a parallel beam. Lenses and reflectors can drastically distort inverse square law approximations, so should be avoided where precision distance calculations are required.
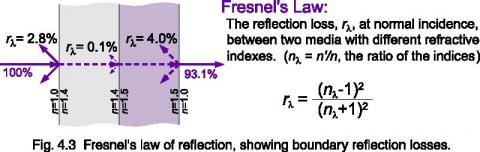
Transmission Losses
When light passes between two materials of different refractive indices, a predictable amount of reflection losses can be expected. Fresnel’s law quantifies this loss. If nλ = 1.5 between air and glass, then rλ = 4% for each surface. Two filters separated by air transmit 8% less than two connected by optical cement (or even water).
Precision optical systems use first surface mirrors to avoid reflection losses from entering and exiting a glass substrate layer.
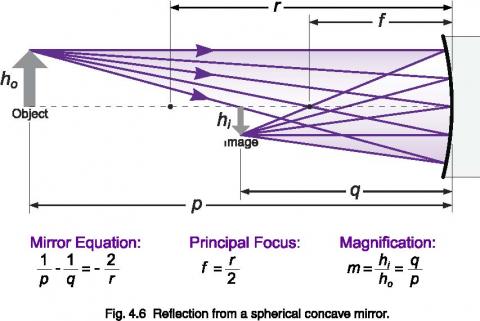
Focusing Lenses
Lenses are often employed to redirect light or concentrate optical power. The lens equation defines the image distance q, projected from a point that is a distance p from the lens, based on the focal distance, f, of the lens. The focal distance is dependent on the curvature and refractive index of the lens.
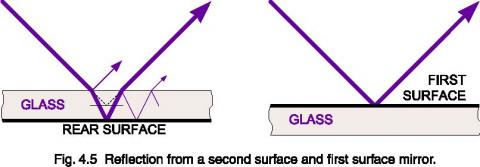
First surface mirrors avoid this by aluminizing the front, and coating it with a thin protective SiO coating to prevent oxidation and scratching.
Concave Mirrors
Concave mirrors are often used to focus light in place of a lens. Just as with a lens, a concave mirror has a principal focus, f, through which all rays parallel to the optical axis pass through. The focal length of a spherical concave mirror is one half the radius of the spherical surface. Reflective systems avoid the chromatic aberrations that can result from the use of lenses.
Internal Transmittance
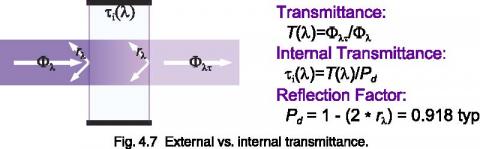
Filter manufacturers usually provide data for a glass of nominal thickness. Using Bouger’s law, you can calculate the transmission at other thicknesses. Manufacturers usually specify Pd, so you can calculate the external transmittance from internal transmittance data.
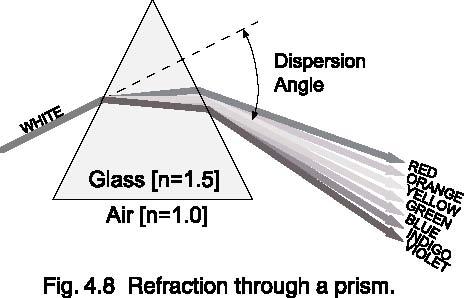
Prisms
Prisms use glass with a high index of refraction to exploit the variation.
of refraction with wavelength. Blue light refracts more than red, providing a spectrum that can be isolated using a narrow slit.
Internal prisms can be used to simply reflect light. Since total internal reflection is dependent on a difference in refractive index between materials, any dirt on the outer surface will reduce the reflective properties, a property that is exploited in finger print readers.
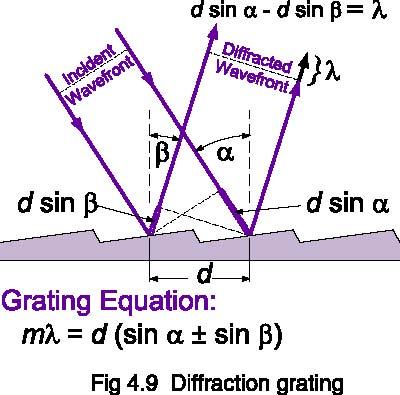
Diffraction Gratings
Most monochromators use gratings to disperse light into the spectrum. Gratings rely on interference between wavefronts caused by microscopically ruled diffraction lines on a mirrored surface. The wavelength of reflected light varies with angle, as defined by the grating equation, where m is the order of the spectrum (an integer).

Request Light Management Handbook as PDF (ALL Chapters)
Chapter 4 - The Light Measurement Handbook
Copyright © 1997 by Alexander D. Ryer
All Rights Reserved.
No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system, without permission in writing from the copyright owner. Requests should be made through the publisher.
Technical Publications Dept.
International Light Technologies
10 Technology Drive
Peabody, MA 01960
ISBN 0-9658356-9-3
Library of Congress Catalog Card Number: 97-93677
Explore more light measurement resources
